As explained in our previous article, growing a model in most dimensions in quite simple, but increasing the hidden size comes with a few problems. This article dives deep and shows how it can be done.
Why, again?
We can simply grow a model’s MLP (intermediate size) or number of layers, without altering loss. This can be done by increasing matrix sizes and padding with zeros (for MLP) or adding all-zero matrices even (for additional layers). This will, however, lead to a model that is not in balance, if we don’t also grow in the hidden size dimension. We assume this is not optimal for training. The underlying mathematical implementation of a model makes increasing the hidden size dimension, while keeping loss equal, far more complicated than increasing size in other dimensions. Some more things need to change along with the hidden size.
Sidenotes:
- The Python code in this article can be easily selected for copy&paste; the prompt, output and comments are excluded from selection.
- This article uses a StableLm model as an example, but applies, mutatis mutandis, to similar models.
- Growing a model with zeros is just step one; the new parameters need non-zero initialization to be trainable.
- This article doesn’t explain how to handle models with
num_key_value_heads != num_attention_heads.
A quick recap
Our previous article already explained that one problem lies in the line doing .mean() here, in LayerNorm code taken from Llama:
def forward(self, hidden_states):
input_dtype = hidden_states.dtype
hidden_states = hidden_states.to(torch.float32)
variance = hidden_states.pow(2).mean(-1, keepdim=True)
hidden_states = hidden_states * torch.rsqrt(variance + self.variance_epsilon)
return self.weight * hidden_states.to(input_dtype)This is because this line can be written as:
variance = hidden_states.pow(2).sum(-1, keepdim=True)/hidden_sizeand it is easy to see that adding zeros keeps the sum equal, but increasing hidden size reduces the variance value calculated, directly impacting the values returned by this forward(), by (implicitly) scaling them with a factor of sqrt(hidden_new/hidden_old).
Solving the problem within existing model code
We think it is best to solve this by modifying the code, but that breaks compatibility. To solve it, approximately, within existing model code, the values of self.weight of LayerNorm objects may be scaled appropriately. Another thing to watch out for is that the q_proj, k_proj and v_proj matrices are actually used (indirectly) as 3D matrices, with one dimension of hidden_size reshaped in two dimensions of sizes head_dim and num_key_value_heads, with head_dim = hidden_size / num_key_value_heads. We will get back to that.
Let’s first naively create a bigger model and see what happens:
$ python -i
1644515328
StableLmForCausalLM(
(model): StableLmModel(
(embed_tokens): Embedding(100352, 2560)
(layers): ModuleList(
(0-23): 24 x StableLmDecoderLayer(
(self_attn): StableLmFlashAttention2(
(q_proj): Linear(in_features=2560, out_features=2560, bias=True)
(k_proj): Linear(in_features=2560, out_features=2560, bias=True)
(v_proj): Linear(in_features=2560, out_features=2560, bias=True)
(o_proj): Linear(in_features=2560, out_features=2560, bias=False)
(attention_dropout): Dropout(p=0.0, inplace=False)
(rotary_emb): StableLmRotaryEmbedding()
)
(mlp): StableLmMLP(
(gate_proj): Linear(in_features=2560, out_features=5632, bias=False)
(up_proj): Linear(in_features=2560, out_features=5632, bias=False)
(down_proj): Linear(in_features=5632, out_features=2560, bias=False)
(act_fn): SiLU()
)
(input_layernorm): LayerNorm((2560,), eps=1e-05, elementwise_affine=True)
(post_attention_layernorm): LayerNorm((2560,), eps=1e-05, elementwise_affine=True)
(dropout): Dropout(p=0.0, inplace=False)
)
)
(norm): LayerNorm((2560,), eps=1e-05, elementwise_affine=True)
)
(lm_head): Linear(in_features=2560, out_features=100352, bias=False)
)
536957952 So we succeeded in adding 537M parameters by increasing hidden_size. These 537M parameters are all accounted for by simple arithmetic:
536957952 Transferring parameters
The new model is initialized with random data, which clearly shows in the loss. We use the Python license text as a sample of English text for loss calculations:
0.7734375
12.125 The low loss of the original model shows that the license text is highly predictable. The high loss of the grown model is expected, for random initialization. Now let’s plug in the parameters of the original model, padded with zeros, and see what happens to the loss:
8.8125 That’s a huge loss increase; maybe better than random initialization, but nowhere near the original score. The problem lies in the way the attention blocks use their projection matrices.
Fixing attention
The issue is that while the q_proj, k_proj and v_proj matrices are 2D, and after projecting hidden_states, result in 2D matrices query_states, key_states and value_states, these states are subsequently used as 4D matrices.
Their shape is (batch_size, sequence_length, num_key_value_heads, head_dim), where num_key_value_heads follows from config and head_dim = hidden_size / num_key_value_heads. To properly grow these projection matrices without changing the resulting 4D state matrices, aside from padding some zeros, they would need to be reshaped to 3D, then grown, and shaped back.
The equivalent attention code
To understand what transformations need to be done, the attention calculations can be analyzed. The easiest way to understand them (for StableLm) is by looking at the Python un-optimized attention implementation in class StableLmAttention, which is what is run with attn_implementation="eager". Only what happens in forward() is relevant, and of that, only those lines matter that stand between incoming and outgoing hidden_states, with dependence on (the shape of) q_proj, k_proj and v_proj. Trimmed down and simplified, the equivalent code looks like this:
hidden_size = 2048 # becomes 2560
num_heads = 32 # from config
batch_size = 1 # to keep it simple
seq_len = ... # arbitrary value
head_dim = hidden_size//num_heads
hidden_states.shape = (batch_size,seq_len,hidden_size)
self.[qkvo]_proj.shape = (hidden_size,hidden_size)
query_states = self.q_proj(hidden_states)
key_states = self.k_proj(hidden_states)
value_states = self.v_proj(hidden_states)
query_states = query_states.view(batch_size, seq_len, num_heads, head_dim).transpose(1, 2)
key_states = key_states.view(batch_size, seq_len, num_heads, head_dim).transpose(1, 2)
value_states = value_states.view(batch_size, seq_len, num_heads, head_dim).transpose(1, 2)
attn_weights = torch.matmul(query_states, key_states.transpose(2, 3)) / math.sqrt(head_dim)
attn_output = torch.matmul(attn_weights, value_states)
attn_output = attn_output.transpose(1, 2)
attn_output = attn_output.reshape(batch_size, seq_len, hidden_size)
hidden_states = self.o_proj(attn_output)The goal is to expand the projection matrices with zeros at the right places, so that hidden_states is effectively expanded with zeros, both on input and output of the attention block. That way, the entire model will give the same loss for the same input (plus, of course, the numerical error originating in necessary scaling), as the other parts of the model are easily adapted to a larger hidden_size by simply extending matrices with zeros.
Note that self.*_proj are linear projections; they are torch objects of type torch.nn.Linear performing a matrix multiplication (with 2D weights) and an addition (with 1D biases). In the following code we will simply perform the matrix multiplications and additions, instead of instantiating these objects, for clarity.
Cracking the transformation problem
Note that not only hidden_size is increased, but also the product num_key_value_heads * head_dim. As we did not modify num_key_value_heads in the config, head_dim increased from 2048/32=64 to 2560/32=80. It is easily seen that this doesn’t play out well in the code shown above. Using smaller numbers to more clearly demonstrate the point, in a toy model:
tensor([[[[1, 2],
[3, 4],
[5, 6],
[7, 8]]]])
tensor([[[[1, 2, 3],
[4, 5, 6],
[7, 8, 0],
[0, 0, 0]]]]) Comparing the two tensors shown, it is obvious that the contents of queries, keys and values are shuffled beyond recognition here, essentially because head_dim has grown from 2 to 3, without inserting zeros at the right place. However, if we choose to keep head_dim equal, and increase num_key_value_heads, things are better:
tensor([[[[1, 2],
[3, 4],
[5, 6],
[7, 8],
[0, 0],
[0, 0]]]]) This looks like it may work out, as the value (and by extension, query and key) state matrices are padded with zeros in one dimension. It is reasonable to expect that this zero padding ends up as zero padding in the resulting hidden_states, even without checking all remaining steps in the attention code.
Solution 1: increase num_heads
The analysis above points to one possible solution: increase num_key_value_heads and num_attention_heads in model.config so that keys, values and queries are simply expanded with zeros as we intended in the first place. Repeating the model creation, but with two additional lines:
0.96875 That’s a 25% hit on the loss; a lot better than random initialization but not yet close to the original score. It is close enough to assume all numbers are in the right place, so let’s see what more needs to be done.
Scaling LayerNorms
We did not account for the change in variance calculation as described above. Let’s try to fix it; in every LayerNorm the variance value goes down as the hidden_size goes up; the hidden_state is multiplied by torch.rsqrt(variance) and this should be compensated in weight:
0.77734375 That’s a 0.5% higher loss than the original model. The exact increase of loss seems to depend on model type, geometry, and sample content, but in general you can expect a loss increase in the order of 1%. In the model code no other factors depend on hidden_size or num_key_value_heads, so this is as good as it gets if we don’t touch the model code.
Solution 2: increase head_dim
We can also increase head_dim. At bit more work, but it can be done. Picking up the small numbers example where we left off, and searching for the way we would have wanted it to look like, that is, expanding a 4D matrix with zeros and shaping it back:
tensor([[[[1, 2, 0],
[3, 4, 0],
[5, 6, 0],
[7, 8, 0]]]])
tensor([[[1, 2, 0, 3, 4, 0, 5, 6, 0, 7, 8, 0]]]) It is immediately clear that zeros are inserted in value_states in its lower dimensional form, when head_dim is increased, and no trivial padding of zeros in v_proj would do that. Expanding our toy example upward towards some hypothetical hidden_states and v_proj shows the way to go. Let’s first get from some hidden_states to the point we ended up before, with a naively padded v_proj and v_bias:
tensor([11, 12, 13, 14, 15, 16, 17, 18])
tensor([11, 12, 13, 14, 15, 16, 17, 18, 0, 0, 0, 0])
tensor([[[[11, 12, 13],
[14, 15, 16],
[17, 18, 0],
[ 0, 0, 0]]]]) The problem clearly lies in how v_proj_grown is derived from v_proj, and using the same reshape-and-extend logic as before, but now applied to v_proj, we can fix it:
tensor([[[1, 0, 0, 0, 0, 0, 0, 0],
[0, 1, 0, 0, 0, 0, 0, 0]],
[[0, 0, 1, 0, 0, 0, 0, 0],
[0, 0, 0, 1, 0, 0, 0, 0]],
[[0, 0, 0, 0, 1, 0, 0, 0],
[0, 0, 0, 0, 0, 1, 0, 0]],
[[0, 0, 0, 0, 0, 0, 1, 0],
[0, 0, 0, 0, 0, 0, 0, 1]]])
expand in the head_dim dimension
expand in the hidden_size dimension
tensor([[[1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]],
[[0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]],
[[0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]],
[[0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]]]) And now to see if it indeed produces the desired outcome:
tensor([[1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]])
tensor([11, 12, 10, 13, 14, 10, 15, 16, 0, 7, 8, 0])
tensor([[[[11, 12, 10],
[13, 14, 10],
[15, 16, 0],
[ 7, 8, 0]]]]) Almost there: because the reshaping of the projection matrices in 3D introduces new rows in the 2D form, equivalent zeros need to be inserted in the bias vectors:
tensor([10, 10, 0, 10, 10, 0, 10, 10, 0, 10, 10, 0])
tensor([11, 12, 0, 13, 14, 0, 15, 16, 0, 17, 18, 0])
tensor([[[[11, 12, 0],
[13, 14, 0],
[15, 16, 0],
[17, 18, 0]]]]) So far, so good! We worked our way up from value_states to see what needed to be done to v_proj (and, by extension, to q_proj and k_proj), but still need to check what happens on the way down to attn_output.
Intermezzo: a minor simplification
Extending the 2D/3D matrices as done above, is a bit verbose and clutters the code. We will use this function in the code that follows:
This code exploits the fact that reshaping and creating a view amount to the same folding of matrix values.
Working our way down to attn_output
As queries, keys and values are all derived in the same way from hidden_states, and have their padded zeros on the same locations, in our toy model we can simply use value_states_grown for each of the state matrices and see where the zeros end up.
tensor([[[[ 2915, 3180, 0]],
[[ 4745, 5110, 0]],
[[ 7215, 7696, 0]],
[[10421, 11034, 0]]]])
tensor([[[ 2915, 3180, 0, 4745, 5110, 0, 7215, 7696, 0, 10421, 11034, 0]]]) This attn_output matrix is then projected using o_proj, for which we will use an identity matrix like we did for v_proj. Let’s first see what happens if we naively grow o_proj to hidden_size_grown, padding with zeros:
tensor([[[ 2915, 3180, 0, 4745, 5110, 0, 7215, 7696, 0, 0, 0, 0]]]) This clearly cuts off some values (note that 10421 and 11034 are gone), and leaves zeros in, where it should ideally re-arrange the matrix so that the padding is at the end – the end goal being that the attention block outputs the same hidden_states as before, but padded. We need to do the inverse of what we did going from v_proj to v_proj_grown to reverse the insertion of zeros. The attention code doesn’t make the higher dimensional nature of o_proj explicit, but as it is the inverse operation of the other projection matrices, we can make an educated guess and follow the same steps as before for v_proj. We also have to realise that o_proj needs to be transposed to get the inserted zeros on the right dimension, with the net result that, in addition to the modifications derived above, only two transpositions (.T) need to be done:
tensor([[1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]]) And now for the final test:
tensor([[[ 2915, 3180, 4745, 5110, 7215, 7696, 10421, 11034, 0, 0, 0, 0]]]) Which is what we were looking for. The attention block now takes hidden_states padded with zeros, and returns hidden_states padded with zeros. The above of course only shows it works for the special mix of identity and all-one matrices; the same steps can be repeated with matrices filled with random numbers and the conclusions will hold.
The toy example now works out, but can we use the above to fix the grown model?
Increasing head_dim in the model
Here we create the bigger model, and iterate over the parameters to copy them, possibly altering them in the process:
0.91015625 This is only 18% worse than the original.
Note that we reduced the partial_rotary_factor, so that the number of head_dim rows to which rotary embedding is applied remains equal:
self.rotary_ndims = int(self.head_dim * config.partial_rotary_factor)After deriving key_states and value_states, these states are cut in two parts, and on one part (of size self.rotary_ndims) rotary position embedding is applied, to finally concatenate the parts back together.
We skipped a few additional important details. One of them is the scaling of LayerNorms described before:
0.8125 This is 5% worse than the original. Another factor is the scaling by math.sqrt(head_dim) which we need to account for, which we do by increasing either k_proj or q_proj, as the scaling is done on the matrix product of key_states and query_states.
0.77734375 This value is 0.5% above the original loss value, in line with the result achieved through increasing the number of heads.
Solution 3: hybrid approaches
Of course it is also be possible to combine both solutions, and increase both num_heads and head_dim, e.g. 36 heads with a head dimension of 71, for a hidden_size of 2556. The creation of such a model is left as an exercise to the reader – the end result is, again, 0.5% loss increase.
Sanity check: is it all about numerical precision?
It may be tempting to think that higher precision would allow models to grow and keep the same loss. This is tested by increasing precision and repeating the process, and it turns out numerical precision does not fully explain the additional loss. Repeating the above steps with float32 shows that the loss is still 0.4% higher for the bigger model.
The reason for this is that StableLm uses nn.LayerNorm for normalization, which, in addition to the LayerNorm.forward() quoted above from Llama, subtracts the mean of the hidden states, before normalizing the magnitude using the variance:
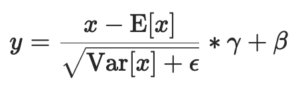
x denotes hidden_states, E[x] is equivalent to x.sum()/hidden_size, and Var[x] to (x-E[x]).pow(2).sum()/hidden_size. Increasing hidden_size by padding hidden_states with zeros proportionally decreases E[x]. There is no way to compensate the change in x-E[x] with changes to parameters alone, if E[x] is non-zero: as the hidden size increases, the mean value E[x] decreases, and Var[E] changes in unpredictable ways. (In Llama models, -E[x] is omitted and the increase in hidden_size can be compensated by appropriately scaling the weights γ).
Here is an attempt to fix this issue in StableLm, by implementing a local clone of nn.LayerNorm that keeps calculations equal to the model before it was grown, by hardcoding the divisor and only applying subtraction on the original, non-zero part of hidden_states:
class StableLmLayerNorm(nn.Module):
def __init__(self, hidden_size, eps=1e-5):
super().__init__()
self.hidden_size = hidden_size
self.eps = eps
self.weight = nn.Parameter(torch.ones(hidden_size))
self.bias = nn.Parameter(torch.zeros(hidden_size))
def forward(self,hidden_states):
hs_orig = 2048
mask = torch.zeros_like(hidden_states)
mask[:,:,:hs_orig] = 1
hidden_states = hidden_states - mask * hidden_states.sum(dim=-1,keepdim=True)/hs_orig
variance = hidden_states.pow(2).sum(dim=-1,keepdim=True)/hs_orig
hidden_states *= torch.rsqrt(variance+self.eps)
hidden_states *= self.weight
hidden_states += self.bias
return hidden_statesUsing this version of LayerNorm instead of nn.LayerNorm indeed allows us to grow the model without any loss increase. The model will of course now rely on this code and will not be compatible with the regular transformers code base.
Conclusion
It is possible to grow a model in the hidden size dimension, and doing so leads to a model performing slightly worse than the original model, with more capacity to train. Further research is needed to determine the optimum between the number of heads and the head dimension, the product of which is the hidden size.
It is clear that numerical error induced by growing is a significant source of additional loss; but even with increased precision, implementation details can cause additional loss as well. These details can be patched, leading to (incompatible) models that can be grown without loss. These findings hint to areas of interest, both regarding efficient training and model optimization in general.
0 Comments